깊이 우선 탐색 vs 너비 우선 탐색
Intro
현재 'do it! 알고리즘 코딩 테스트' 책으로 공부 중인데 그래프 탐색 문제만 나오면 해당 문제가 깊이 우선탐색을 해야 하는지 너비 우선 탐색을 해야 하는지 자꾸만 헷갈린다.
다 풀고 답을 확인해보면 너비 우선으로 풀었어야 할 문제를 깊이 우선으로 푸는 바람에 시간초과가 난다거나, 너비 우선으로 풀어서 답이 도출되지 않아 확인해 보니 깊이우선으로 풀었어야 한다거나...(이건 그냥 내가 잘못 푼 듯ㅎ)
공부가 덜 됐구나 생각이 들어서 오늘은 깊이 우선 탐색과 너비 우선 탐색을 비교하고, 어떤 문제에 어떠한 탐색 방식을 사용해야 하는지 알아보려 한다.
깊이 우선 탐색(Depth-First Search, DFS)
깊이 우선 탐색이란 선택된 첫 노드를 시작으로 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식이다.
참고 자료를 보니 굉장히 좋은 예시가 있었다.
미로 찾기를 할 때 최대한 한 방향으로 갈 수 있을 때까지 쭉 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 그 갈림길부터 다시 다른 방향으로 탐색을 진행하는 것이 깊이 우선 탐색 방식이라고 할 수 있다.
위의 설명대로 전체노드, 모든 분기를 순차적으로 확인해야 할 때는 깊이 우선 탐색을 사용해야 하는 것이고 이 부분은 헷갈리는 것이 없다.
너비 우선 탐색(Breadth-First Search, BFS)
너비 우선 탐색이란 선택된 첫 노드를 시작으로 인접한 노드를 먼저 탐색하는 방식이다.
두 노드 사이의 최단 경로를 찾고 싶을 때 이 방법을 선택한다고 하는데 이유를 모르겠다. (맨날 코테 풀 때 깊이우선 탐색을 사용해서 시간초과가 남ㅠ)
도대체 깊이 우선 탐색은 외않되?
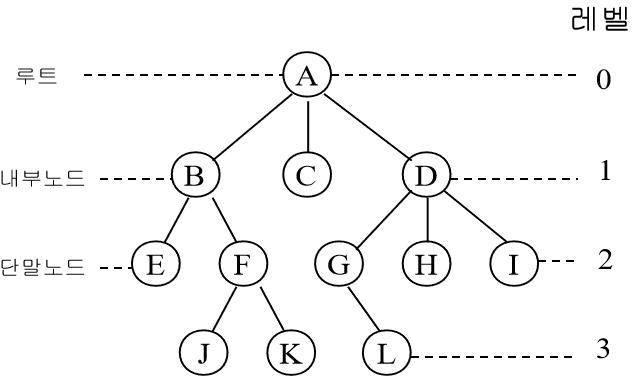
위의 이미지에서 A 노드에서부터 거리가 가장 짧은 친구들을 찾는다고 가정하자.
깊이 우선탐색으로 처리한다면?
A→B→E : 2번 이동
A→B→F→J : 3번 이동
A→B→F→K : 3번 이동
A→C : 1번 이동
A→D→G→L : 3번 이동
A→D→H : 2번 이동
A→H→I : 2번 이동
오 이제 탐색이 끝났군ㅎ
전체 이동 횟수들을 좀 비교해 봐야겠어ㅎ
A에서 C로 갈 때 가장 적게 움직였으니까 A-C로 도출!
⇒ 총 13번 탐색
깊이 우선으로 탐색했을 경우 전체 간선의 수만큼 확인을 한 후 결과가 도출이 된다.
만약 문제가 '한번 이동했을 때의 노드가 단말노드(자식노드)를 가지고 있지 않은 노드를 찾아라!' (너비우선탐색 쓰면 된다) 였다면 물론 탐색 시간이 훨씬 적게 걸렸을 것이다.
하지만 위의 경우 해당 노드에서 가장 거리가 짧은 노드를 찾는 문제이고, 그 거리가 주어진 것은 아니기 때문에 모든 노드들을 방문해서 확인한 후에 '아하 A-C가 가장 짧은 노드구나~' 하고 알게 될 수밖에 없다.
너비 우선 탐색으로 처리한다면?
A→B : 1번 이동
A→C : 1번 이동
A→D : 1번 이동
B→E : 1번 이동
B→F : 1번 이동
C ?? : 오? 단말노드가 없네?ㅎ
D→G : 1번 이동
D→H : 1번 이동
D→I : 1번 이동
오 이미 단말 노드가 없는 노드를 찾아냈으니 탐색을 끝내야겠군ㅎ
단말 노드가 없는 A-C 도출!!
⇒ 총 9번 탐색 (오? 단말노드 없네? 까지 포함)
만약 문제가 '최단거리의 노드들 중 가장 처음으로 찾은 노드를 출력해라!!!!!!'와 같은 문제였다면 물론 더 빠르게 탐색이 끝났을 수도 있겠다. 하지만 위의 문제는 '최단 거리의 노드를 찾아라!!' 였기 때문에 해당 단말 노드가 없는 노드를 찾아냈음에도 해당 레벨의 노드들을 모두 탐색한 후 종료되었다.
그래도 깊이우선탐색보다는 훨씬 빠르다.
결론
깊이 우선탐색의 경우 연결된 전체 간선만큼을 탐색하게 되고, 너비우선 탐색의 경우 트리의 레벨 단위로 확인하기 때문에 위의 문제 같은 경우는 너비우선탐색이 훨씬 빠른 탐색으로 종료된다.
실제 코딩테스트에서는 위의 트리의 개수만큼 호락호락하게 나오지 않으므로 그 탐색 속도는 더 크게 차이가 날 것이다.
하지만 위의 탐색 과정을 적어보며 들었던 생각이 트리의 구조에 따라서도 깊이 우선 탐색이 너비 우선 탐색과 속도가 비슷할 때도 있겠다 생각이 들었다. 이진트리 구조의 경우가 그렇겠다 생각했다.
여튼! 두 노드사이의 최단 경로를 찾는 문제는 특별한 경우를 제외하고는 너비 우선 탐색이 훠얼~~~씬 빠르다는 결론을 도출해냈다.
이제 코테 풀 때 헛다리 짚지 않고 잘 풀 수 있을 것만 같다.ㅎ
참고